- Introduction
- Data import and overview
- Data wrangling
- Model evaluation
- Random forests
- XGBoost
- Conclusion
- Appendix: Catboost
Introduction
This tutorial will go through the steps to make an initial submission to Kaggle competition House Prices - Advanced Regression Techniques available at https://www.kaggle.com/c/house-prices-advanced-regression-techniques, using R for the analysis.
This competition is currently in the Getting Started Prediction category at Kaggle, there are no prizes to win, but it can be a great exercise for getting comfortable working with tabular data. I find that although (or because of?) it is an older competition, Kaggle competitions can be pretty competitive, and while the main focus of this tutorial is learning, I hope that this tutorial also could provide a good starting point for anyone new to this dataset intending to reach for higher scores. In summary this tutorial will cover
- Basic data manipulation with dplyr.
- Feature selection using recursive feature elimination.
- Handling missing values using Random Forests with the package missForest.
- Obtaining predictions using Random Forests and XGBoost.
I will be as explicit as possible regarding parameter values, models and corresponding score on Kaggle, providing a baseline for the reader to improve upon.
Note that in order to retrieve the data for this competition you need to register for a free Kaggle account and join this competition at the Kaggle website.
Getting started with Kaggle
If you are new to Kaggle, you can create a free account at kaggle.com, and register for the competition you want to participate in, for this tutorial you want to register for: House Prices - Advanced Regression Techniques.
The next step is to create a notebook on the Kaggle website with your solution (at the time of writing they support either R or Python notebooks), run it at their servers, and submit your solution to get the score on the test set for the leaderboard. You could also use the command line interface (CLI) to submit your solution, running your code at your own computer, or at a cloud computing service of choice.
| Apart from the competition covered here, I found that the Titanic dataset is a good starting point, with many great tutorials available online. I recommend watching the official Kaggle introduction for the Titanic dataset on youtube, as a gateway to making your first submission: [How to Get Started with Kaggle’s Titanic Competition | Kaggle](https://youtu.be/8yZMXCaFshs). |
Personally, I prefer using the Kaggle CLI rather that the website, the CLI provides a quick and convenient way of interacting with Kaggle, making submissions, signing up for competitions, etc (you can send up to a total of 10 submissions/day using the website and CLI). Check out the official Kaggle documentation for their CLI here: How to Use Kaggle
The Ames Housing data
The dataset for this challenge consists of sale prices of residential property in Ames, Iowa, US, between 2006 and 2010. In total there are 2919 observations (rows) and 81 variables (columns) both numerical, categorical and discrete. The independent variable which we want to predict is the sale price in US dollars.
The result will be evaluated by Kaggle with the root mean squared error between the logarithmised price of the prediction you submit and the true sale price. The submission file should have two columns: property ID and SalePrice, for more details check out https://www.kaggle.com/c/house-prices-advanced-regression-techniques.
dplyr and DescTools
We will begin with loading both the test/train data and join them to make sure we do all initial data wrangling on all the data. We will make use of the dplyr package and Desctools, so we start by importing these, you might need to install them with e.g. Install.packages(“package_name”).
require("dplyr")
require("DescTools")
require("tidyr") # included in tidyverse and required for pivot_longer() used later
Data import and overview
Importing the data
Now we load the test/train data, which I have downloaded from the Kaggle site and placed in the same working directory as this script. Then, we merge the test and training data to one larger dataset to make sure we do all preprocessing/data wrangling on the complete dataset.
We also save the id’s of all observations in the test data to keep track of what is train and what is test.
train_orig = read.csv("train.csv", stringsAsFactors = T) # read training data
test_orig = read.csv("test.csv", stringsAsFactors = T) # read test data
test_id = test_orig$Id # get ID of rows corresponding to the test data
all_data = full_join(train_orig, test_orig) # join test/train data (this works since test/train have exactly the same type of columns)
Now, define a convenience function to get back the test and train sets from the full merged data set, and check the resulting number of rows and columns of our data.
get_tt = function(df){
train = df %>% filter(!(Id %in% test_id)) %>% mutate(Id=NULL)
test = df %>% filter(Id %in% test_id) %>% mutate(Id=NULL)
return(list("train" = train, "test" = test))
}
res = get_tt(all_data)
cat("#Columns in data:", ncol(all_data), "\n")
## #Columns in data: 81
cat("#Rows in training data:", nrow(all_data), "\n")
## #Rows in training data: 2919
cat("#Rows in training data:", nrow(res$train), "\n")
## #Rows in training data: 1460
cat("#Rows in test data:",nrow(res$test), "\n")
## #Rows in test data: 1459
Overview of the data
We start by plotting the distribution of the dependent variable SalePrice, where we note that the distribution seems skewed towards the left.
hist(main="SalePrice", all_data$SalePrice, xlab="SalePrice ($)")
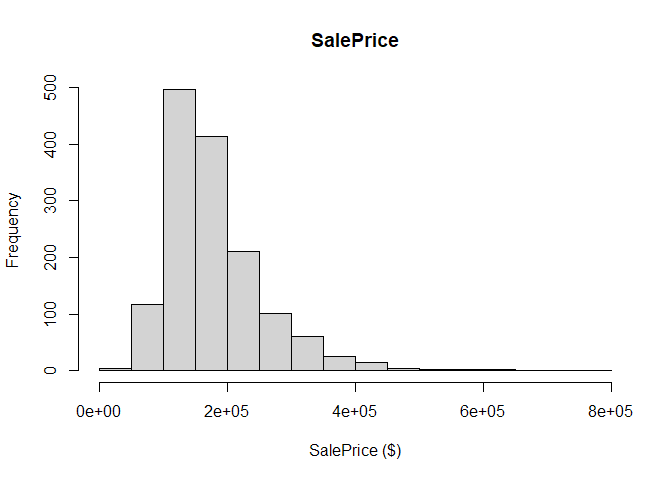
Interestingly, if we instead plot the log of the SalePrice, the distribution looks more normal, providing further motivation for using the logarithmised sale price rather than the value in dollars.
hist(main="SalePrice (log)", log(all_data$SalePrice), xlab="SalePrice (log)")
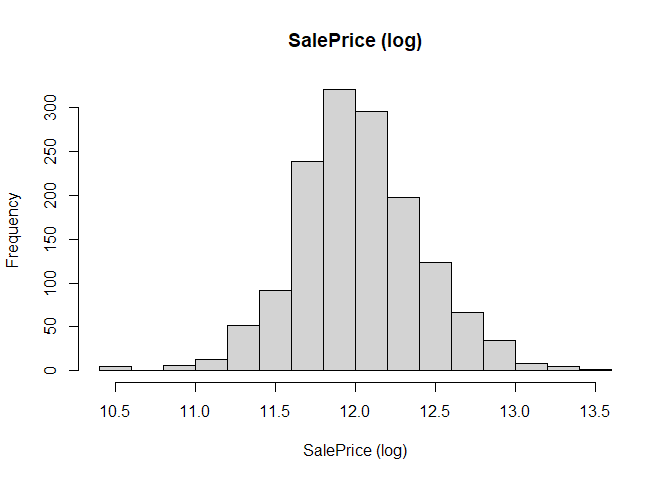
Now, with DescTools, we can get an overview of the whole dataset. The function Desc gives a summary of each variable, depending on the data type. As it gives us a very long list of output, we will instead use Abstract which only lists all variables with their name, type, missing values, along with the different levels for factors (Abstract is otherwise also printed by Desc)
#Desc(all_data, plotit=FALSE) # maybe too much information
Abstract(all_data, list.len=100)
## -----------------------------------------------------------------------------------------------------------------------------------------
## all_data
##
## data frame: 2919 obs. of 81 variables
## 0 complete cases (0.0%)
##
## Nr ColName Class NAs Levels
## 1 Id integer .
## 2 MSSubClass integer .
## 3 MSZoning factor 4 (0.1%) (5): 1-C (all), 2-FV, 3-RH, 4-RL, 5-RM
## 4 LotFrontage integer 486 (16.6%)
## 5 LotArea integer .
## 6 Street factor . (2): 1-Grvl, 2-Pave
## 7 Alley factor 2721 (93.2%) (2): 1-Grvl, 2-Pave
## 8 LotShape factor . (4): 1-IR1, 2-IR2, 3-IR3, 4-Reg
## 9 LandContour factor . (4): 1-Bnk, 2-HLS, 3-Low, 4-Lvl
## 10 Utilities factor 2 (0.1%) (2): 1-AllPub, 2-NoSeWa
## 11 LotConfig factor . (5): 1-Corner, 2-CulDSac, 3-FR2, 4-FR3, 5-Inside
## 12 LandSlope factor . (3): 1-Gtl, 2-Mod, 3-Sev
## 13 Neighborhood factor . (25): 1-Blmngtn, 2-Blueste, 3-BrDale, 4-BrkSide, 5-ClearCr, ...
## 14 Condition1 factor . (9): 1-Artery, 2-Feedr, 3-Norm, 4-PosA, 5-PosN, ...
## 15 Condition2 factor . (8): 1-Artery, 2-Feedr, 3-Norm, 4-PosA, 5-PosN, ...
## 16 BldgType factor . (5): 1-1Fam, 2-2fmCon, 3-Duplex, 4-Twnhs, 5-TwnhsE
## 17 HouseStyle factor . (8): 1-1.5Fin, 2-1.5Unf, 3-1Story, 4-2.5Fin, 5-2.5Unf, ...
## 18 OverallQual integer .
## 19 OverallCond integer .
## 20 YearBuilt integer .
## 21 YearRemodAdd integer .
## 22 RoofStyle factor . (6): 1-Flat, 2-Gable, 3-Gambrel, 4-Hip, 5-Mansard, ...
## 23 RoofMatl factor . (8): 1-ClyTile, 2-CompShg, 3-Membran, 4-Metal, 5-Roll, ...
## 24 Exterior1st factor 1 (0.0%) (15): 1-AsbShng, 2-AsphShn, 3-BrkComm, 4-BrkFace, 5-CBlock, ...
## 25 Exterior2nd factor 1 (0.0%) (16): 1-AsbShng, 2-AsphShn, 3-Brk Cmn, 4-BrkFace, 5-CBlock, ...
## 26 MasVnrType factor 24 (0.8%) (4): 1-BrkCmn, 2-BrkFace, 3-None, 4-Stone
## 27 MasVnrArea integer 23 (0.8%)
## 28 ExterQual factor . (4): 1-Ex, 2-Fa, 3-Gd, 4-TA
## 29 ExterCond factor . (5): 1-Ex, 2-Fa, 3-Gd, 4-Po, 5-TA
## 30 Foundation factor . (6): 1-BrkTil, 2-CBlock, 3-PConc, 4-Slab, 5-Stone, ...
## 31 BsmtQual factor 81 (2.8%) (4): 1-Ex, 2-Fa, 3-Gd, 4-TA
## 32 BsmtCond factor 82 (2.8%) (4): 1-Fa, 2-Gd, 3-Po, 4-TA
## 33 BsmtExposure factor 82 (2.8%) (4): 1-Av, 2-Gd, 3-Mn, 4-No
## 34 BsmtFinType1 factor 79 (2.7%) (6): 1-ALQ, 2-BLQ, 3-GLQ, 4-LwQ, 5-Rec, ...
## 35 BsmtFinSF1 integer 1 (0.0%)
## 36 BsmtFinType2 factor 80 (2.7%) (6): 1-ALQ, 2-BLQ, 3-GLQ, 4-LwQ, 5-Rec, ...
## 37 BsmtFinSF2 integer 1 (0.0%)
## 38 BsmtUnfSF integer 1 (0.0%)
## 39 TotalBsmtSF integer 1 (0.0%)
## 40 Heating factor . (6): 1-Floor, 2-GasA, 3-GasW, 4-Grav, 5-OthW, ...
## 41 HeatingQC factor . (5): 1-Ex, 2-Fa, 3-Gd, 4-Po, 5-TA
## 42 CentralAir factor . (2): 1-N, 2-Y
## 43 Electrical factor 1 (0.0%) (5): 1-FuseA, 2-FuseF, 3-FuseP, 4-Mix, 5-SBrkr
## 44 X1stFlrSF integer .
## 45 X2ndFlrSF integer .
## 46 LowQualFinSF integer .
## 47 GrLivArea integer .
## 48 BsmtFullBath integer 2 (0.1%)
## 49 BsmtHalfBath integer 2 (0.1%)
## 50 FullBath integer .
## 51 HalfBath integer .
## 52 BedroomAbvGr integer .
## 53 KitchenAbvGr integer .
## 54 KitchenQual factor 1 (0.0%) (4): 1-Ex, 2-Fa, 3-Gd, 4-TA
## 55 TotRmsAbvGrd integer .
## 56 Functional factor 2 (0.1%) (7): 1-Maj1, 2-Maj2, 3-Min1, 4-Min2, 5-Mod, ...
## 57 Fireplaces integer .
## 58 FireplaceQu factor 1420 (48.6%) (5): 1-Ex, 2-Fa, 3-Gd, 4-Po, 5-TA
## 59 GarageType factor 157 (5.4%) (6): 1-2Types, 2-Attchd, 3-Basment, 4-BuiltIn, 5-CarPort, ...
## 60 GarageYrBlt integer 159 (5.4%)
## 61 GarageFinish factor 159 (5.4%) (3): 1-Fin, 2-RFn, 3-Unf
## 62 GarageCars integer 1 (0.0%)
## 63 GarageArea integer 1 (0.0%)
## 64 GarageQual factor 159 (5.4%) (5): 1-Ex, 2-Fa, 3-Gd, 4-Po, 5-TA
## 65 GarageCond factor 159 (5.4%) (5): 1-Ex, 2-Fa, 3-Gd, 4-Po, 5-TA
## 66 PavedDrive factor . (3): 1-N, 2-P, 3-Y
## 67 WoodDeckSF integer .
## 68 OpenPorchSF integer .
## 69 EnclosedPorch integer .
## 70 X3SsnPorch integer .
## 71 ScreenPorch integer .
## 72 PoolArea integer .
## 73 PoolQC factor 2909 (99.7%) (3): 1-Ex, 2-Fa, 3-Gd
## 74 Fence factor 2348 (80.4%) (4): 1-GdPrv, 2-GdWo, 3-MnPrv, 4-MnWw
## 75 MiscFeature factor 2814 (96.4%) (4): 1-Gar2, 2-Othr, 3-Shed, 4-TenC
## 76 MiscVal integer .
## 77 MoSold integer .
## 78 YrSold integer .
## 79 SaleType factor 1 (0.0%) (9): 1-COD, 2-Con, 3-ConLD, 4-ConLI, 5-ConLw, ...
## 80 SaleCondition factor . (6): 1-Abnorml, 2-AdjLand, 3-Alloca, 4-Family, 5-Normal, ...
## 81 SalePrice integer 1459 (50.0%)
There is a mixture of numerical and categorical variables, with some categorical variables (factors) having overlapping levels (e.g. GarageQual, GarageCond, FireplaceQu, …). Information of the meaning of all different features and levels can be found on Kaggle.
Importantly, we note several features have missing values, which we want to correct later, but before this we first check for errors related to the data type or input form when loading the data into R.
Data wrangling
Check numerical variables for errors
When loading our data, all non-numerical should have been loaded as Factors in R, while numerical columns are Numeric or integer.
To check if these datatypes makes sense for the respective features, we first look at all numerical variables to see if we can spot any obvious errors, utilizing the capabilities of the dplyr package, calculating mean, min, max and number of unique values for each column.
num_summary = all_data %>%
summarise(across(where(~is.numeric(.)), # do this for numeric columns
list(mean = ~mean(.x, na.rm = TRUE),
min = ~min(.x, na.rm = TRUE),
max = ~max(.x, na.rm = TRUE),
nUnique = ~length(unique(.x, na.rm = TRUE))))) %>%
pivot_longer(cols = everything(),
names_sep = "_",
names_to = c("variable", ".value"))
print(num_summary, n=100)
## # A tibble: 38 x 5
## variable mean min max nUnique
## <chr> <dbl> <int> <int> <int>
## 1 Id 1460 1 2919 2919
## 2 MSSubClass 57.1 20 190 16
## 3 LotFrontage 69.3 21 313 129
## 4 LotArea 10168. 1300 215245 1951
## 5 OverallQual 6.09 1 10 10
## 6 OverallCond 5.56 1 9 9
## 7 YearBuilt 1971. 1872 2010 118
## 8 YearRemodAdd 1984. 1950 2010 61
## 9 MasVnrArea 102. 0 1600 445
## 10 BsmtFinSF1 441. 0 5644 992
## 11 BsmtFinSF2 49.6 0 1526 273
## 12 BsmtUnfSF 561. 0 2336 1136
## 13 TotalBsmtSF 1052. 0 6110 1059
## 14 X1stFlrSF 1160. 334 5095 1083
## 15 X2ndFlrSF 336. 0 2065 635
## 16 LowQualFinSF 4.69 0 1064 36
## 17 GrLivArea 1501. 334 5642 1292
## 18 BsmtFullBath 0.430 0 3 5
## 19 BsmtHalfBath 0.0614 0 2 4
## 20 FullBath 1.57 0 4 5
## 21 HalfBath 0.380 0 2 3
## 22 BedroomAbvGr 2.86 0 8 8
## 23 KitchenAbvGr 1.04 0 3 4
## 24 TotRmsAbvGrd 6.45 2 15 14
## 25 Fireplaces 0.597 0 4 5
## 26 GarageYrBlt 1978. 1895 2207 104
## 27 GarageCars 1.77 0 5 7
## 28 GarageArea 473. 0 1488 604
## 29 WoodDeckSF 93.7 0 1424 379
## 30 OpenPorchSF 47.5 0 742 252
## 31 EnclosedPorch 23.1 0 1012 183
## 32 X3SsnPorch 2.60 0 508 31
## 33 ScreenPorch 16.1 0 576 121
## 34 PoolArea 2.25 0 800 14
## 35 MiscVal 50.8 0 17000 38
## 36 MoSold 6.21 1 12 12
## 37 YrSold 2008. 2006 2010 5
## 38 SalePrice 180921. 34900 755000 664
Comparing the list of numerical variables with the data description on Kaggle, we note that MSSubClass is actually a code for the type of residence (see data description on the Kaggle website), and should be a categorical variable (factor), not a numerical value, therefore we simply convert it to a factor as such, with the levels corresponding to the different residential codes for the type of property:
all_data$MSSubClass = as.factor(all_data$MSSubClass)
Further, at least one house has a garage from the future (GarageYrBlt=2207), lets set this value to the same year (YearBuilt) the house was built. In fact, lets do this for all garages built after 2010 (there is only one row like this though), using the mutate and ifelse functions from dplyr.
all_data = all_data %>%
mutate(GarageYrBlt = ifelse(GarageYrBlt>2010, YearBuilt, GarageYrBlt))
Otherwise, except for the missing values which we save for later, I cannot spot any obvious error in these datasets from this very simple analysis, and we will move on.
Check categorical variables for errors
After looking at the numerical values, we move on to the categorical features in the dataset. We note that categorical values can be any of two following types:
- Ordinal: Categorical variable with intrinsic order, can be placed on a scale. Example: height (short, average, tall).
- Nominal: Categorical variable with no intrinsic order. Example: list of colors (blue, green, red).
For simplicity, we assume all categorical variables to be of the nominal type, despite this obviously not being true. Several of the categorical variables indicate some form of condition/quality ranging from worst to best, and it might be beneficial to leverage this information by converting these to e.g. (ordered) integers, putting these on a scale of what we think is from low to high value/SalePrice. Deeming this to be out of scope for this tutorial, such an exercise is left to the reader, as it seemed possible to get decent results assuming only nominal categories.
Otherwise, a quick comparison of the categorical variables and the data description reveals nothing wrong with any of the categorical variables as far as I can see. It could be that some values are mistyped but this is hard for me to judge, and I will not be modifying any of these values. However, several of the categorical values are still missing, and this is what we will focus on next. # Missing values Shifting our focus to the missing values in the data, we begin defining a function for calculating the percentage of missing values per column, to keep track of our progress:
perc_missing = function(x) colSums(is.na(x)/nrow(x))*100
pm = perc_missing(all_data)
# Missing values (%) per column, descending
print(pm[order(-pm)])
## PoolQC MiscFeature Alley Fence SalePrice FireplaceQu LotFrontage GarageYrBlt GarageFinish
## 99.65741692 96.40287770 93.21685509 80.43850634 49.98287085 48.64679685 16.64953751 5.44707091 5.44707091
## GarageQual GarageCond GarageType BsmtCond BsmtExposure BsmtQual BsmtFinType2 BsmtFinType1 MasVnrType
## 5.44707091 5.44707091 5.37855430 2.80918123 2.80918123 2.77492292 2.74066461 2.70640630 0.82219938
## MasVnrArea MSZoning Utilities BsmtFullBath BsmtHalfBath Functional Exterior1st Exterior2nd BsmtFinSF1
## 0.78794108 0.13703323 0.06851662 0.06851662 0.06851662 0.06851662 0.03425831 0.03425831 0.03425831
## BsmtFinSF2 BsmtUnfSF TotalBsmtSF Electrical KitchenQual GarageCars GarageArea SaleType Id
## 0.03425831 0.03425831 0.03425831 0.03425831 0.03425831 0.03425831 0.03425831 0.03425831 0.00000000
## MSSubClass LotArea Street LotShape LandContour LotConfig LandSlope Neighborhood Condition1
## 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## Condition2 BldgType HouseStyle OverallQual OverallCond YearBuilt YearRemodAdd RoofStyle RoofMatl
## 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## ExterQual ExterCond Foundation Heating HeatingQC CentralAir X1stFlrSF X2ndFlrSF LowQualFinSF
## 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## GrLivArea FullBath HalfBath BedroomAbvGr KitchenAbvGr TotRmsAbvGrd Fireplaces PavedDrive WoodDeckSF
## 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## OpenPorchSF EnclosedPorch X3SsnPorch ScreenPorch PoolArea MiscVal MoSold YrSold SaleCondition
## 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
Except for SalePrice, which we want to predict, we note that only PoolQC, MiscFeature, Alley, Fence, FireplaceQu, LotFrontage have more than 10% missing values, (see official Kaggle description for the meaning of these variables), though there are many columns with some missing values:
cat("Number of columns in data set:", ncol(all_data), "\n")
## Number of columns in data set: 81
cat("Number of columns with NA's:", sum(0 != pm), "\n")
## Number of columns with NA's: 35
Several of the features with missing values will be remedied in the next section, noting that a missing value is actually a special value indicating a feature being absent. After this modification, the remaining missing values will then be imputed with a Random Forest algorithm.
Replacing NA’s with Absent
We note 34 features have missing values, ignoring dependent variable SalePrice.
According to the data description available at the Kaggle website, NA is a special value denoting absent/none for the following categories: FireplaceQu, GarageType, GarageFinish, GarageQual, GarageCond, PoolQC, Fence, MiscFeature, Alley, BsmtQual, BsmtCond, BsmtExposure, BsmtFinType1, BsmtFinType2. In theory it is possible that some of these NA’s actually are true missing values, data which was not collected, but we will follow the description and replace all NA values with the category ‘absent’, meaning that an NA indicate lack of e.g. a basement, garage, for the columns mentioned above.
# define name of columns for which we want to replace NA's with the new category 'Absent'
na_means_absence = c("FireplaceQu", "GarageType", "GarageFinish", "GarageQual", "GarageCond", "PoolQC", "Fence",
"MiscFeature", "Alley", "BsmtQual", "BsmtCond", "BsmtExposure", "BsmtFinType1", "BsmtFinType2")
# helper function for replacing NA's with Absent
fact_replace_na = function(x){
x = as.character(x)
x = if_else(is.na(x), "Absent", x)
x = as.factor(x)
}
# apply 'fact_replace_na' to columns listed in 'na_means_absent'
all_data = all_data %>%
mutate_at(na_means_absence, fact_replace_na)
Now, we have 21 columns with missing values instead of 31:
pm = perc_missing(all_data)
cat("Number of columns with NA's (after replacing NA's with 'absent'):", sum(0 != pm), "\n")
## Number of columns with NA's (after replacing NA's with 'absent'): 21
Check dataset consistency
Let’s do a quick check on the subset of columns defined above to see if the dataset is consistent, by noting that if one of the garage variables indicates an absence, the rest of the garage-related variables should also have the value absent.
garage_c = c("GarageType", "GarageFinish", "GarageQual", "GarageCond")
# extract indices of inconsistent rows (if any)
inconsistent_rows = which(apply(all_data[,garage_c] == "Absent", 1, any) & apply(all_data[,garage_c] != "Absent", 1, any))
all_data[inconsistent_rows,] %>% select(contains("garage"))
## GarageType GarageYrBlt GarageFinish GarageCars GarageArea GarageQual GarageCond
## 2127 Detchd NA Absent 1 360 Absent Absent
## 2577 Detchd NA Absent NA NA Absent Absent
Two observations have a detached (Detchd) GarageType, while other columns indicates absence. It seems possible that a ‘detached’ garage can be seen as also being absent, or semi-absent, depending on how you view it, and here we will keep these data points as they are for the model.
Let’s also look at the basement columns instead and see if they seem consistent.
bsmt_c=c("BsmtQual", "BsmtCond", "BsmtExposure", "BsmtFinType1", "BsmtFinType2")
# extract indices of inconsistent rows (if any)
inconsistent_rows = which(apply(all_data[,bsmt_c] == "Absent", 1, any) & apply(all_data[,bsmt_c] != "Absent", 1, any))
all_data[inconsistent_rows,] %>% select(contains("bsmt"))
## BsmtQual BsmtCond BsmtExposure BsmtFinType1 BsmtFinSF1 BsmtFinType2 BsmtFinSF2 BsmtUnfSF TotalBsmtSF BsmtFullBath BsmtHalfBath
## 333 Gd TA No GLQ 1124 Absent 479 1603 3206 1 0
## 949 Gd TA Absent Unf 0 Unf 0 936 936 0 0
## 1488 Gd TA Absent Unf 0 Unf 0 1595 1595 0 0
## 2041 Gd Absent Mn GLQ 1044 Rec 382 0 1426 1 0
## 2186 TA Absent No BLQ 1033 Unf 0 94 1127 0 1
## 2218 Absent Fa No Unf 0 Unf 0 173 173 0 0
## 2219 Absent TA No Unf 0 Unf 0 356 356 0 0
## 2349 Gd TA Absent Unf 0 Unf 0 725 725 0 0
## 2525 TA Absent Av ALQ 755 Unf 0 240 995 0 0
In total 9 rows show the basement as being absent while some of the other columns indicates that the basement exists, by giving scores for e.g., height (BsmtQual) or condition (BsmtCond). Sometimes a house can have more than one basement with one of them unfinished (=absent?), and I found it difficult to see just from the data what is correct here (which column we should be trust). Since there are only 9 rows it probably won’t to much harm to keep them, and as these values could contain some important signal relating to quality/building progress, therefore I will leave these unchanged.
Considering the size of this dataset (>2900 observations), the sample features we looked at seemed fairly consistent, where Absent-type garages were almost always followed by absent/unfinished/detached status in related columns. For our purposes we will not dig any deeper into this, but we note that some gain might be had by making sure that the entire dataset is consistent, by e.g. changing all related values to absent if at least one value indicates the absence of a feature, or by some other strategy.
Despite this, we will treat the status of our dataset at this point to be “good enough” and we will now move on to impute the rest of the missing values using random forests.
Imputation with missForest
First, we see that although many (=21) features still have missing values, only LotFrontage and GarageYrBlt have more than 1% missing, after replacing NA’s with Absent where applicable according to description (ignoring the target variable SalePrice).
pm = perc_missing(all_data)
print(pm[pm>1]) # more than 1% missing
## LotFrontage GarageYrBlt SalePrice
## 16.649538 5.447071 49.982871
print(pm[pm>0]) # features with missing values
## MSZoning LotFrontage Utilities Exterior1st Exterior2nd MasVnrType MasVnrArea BsmtFinSF1 BsmtFinSF2 BsmtUnfSF
## 0.13703323 16.64953751 0.06851662 0.03425831 0.03425831 0.82219938 0.78794108 0.03425831 0.03425831 0.03425831
## TotalBsmtSF Electrical BsmtFullBath BsmtHalfBath KitchenQual Functional GarageYrBlt GarageCars GarageArea SaleType
## 0.03425831 0.03425831 0.06851662 0.06851662 0.03425831 0.06851662 5.44707091 0.03425831 0.03425831 0.03425831
## SalePrice
## 49.98287085
We will now impute the remaining missing values with the missForest library.
missForest uses random forests to predict values for the NA’s in the dataset. First we load the package, install it if needed (it is available at CRAN).
#install.packages("missForest")
require(missForest)
## Loading required package: missForest
## Loading required package: randomForest
## randomForest 4.6-14
## Type rfNews() to see new features/changes/bug fixes.
##
## Attaching package: 'randomForest'
## The following object is masked from 'package:dplyr':
##
## combine
## Loading required package: foreach
## Loading required package: itertools
## Loading required package: iterators
Important parameters that we will change here the Random Forest algorithm are ntree, the number of trees in each forest, maxiter, the maximum number of iterations, but see also the documentation (the one you get by typing ?missForest in R) for more information.
We will reduce the number of trees to 10 (from 100) and keep maxiter at 10, and having all other parameters at their default values, as this seems to work well for the current problem.
# Impute missing values, excluding the target column (SalePrice)
imp_result = missForest(select(all_data, -SalePrice), maxiter=10, ntree=10) # !!!
## missForest iteration 1 in progress...
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## done!
## missForest iteration 2 in progress...
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## done!
## missForest iteration 3 in progress...
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## done!
## missForest iteration 4 in progress...
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## done!
## missForest iteration 5 in progress...
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## done!
## missForest iteration 6 in progress...
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## done!
## missForest iteration 7 in progress...
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## Warning in randomForest.default(x = obsX, y = obsY, ntree = ntree, mtry = mtry, : The response has five or fewer unique values. Are you
## sure you want to do regression?
## done!
# ' missForest additionally gives us the out-of-bag (OOB) errors calculated by comparing imputed values to
# ' the values in the training data, calculated as the normalized root mean squared error (NRMSE)
# ' for continuous variables and proportion of falsely classified (PFC) for the
# ' categorical variables, providing an indication of the overall imputation error.
imp_result$OOBerror
## NRMSE PFC
## 0.03336438 0.03371619
The error rate introduced by imputation of the missing data is estimated at about 4%, which does not seem to bad. We save this result and verify that no values are missing.
data_imp = imp_result$ximp
cat("Columns with missing values:", sum(0 != perc_missing(data_imp)), "\n")
## Columns with missing values: 0
# add back dependent variable SalePrice to the data
data_imp$SalePrice = all_data$SalePrice
After some rudimentary data cleaning and imputation of missing values we now we have a complete dataset (no missing values), and are ready to move on to the modelling.
Model evaluation
We will model the data with both Random Forests and XGBoost. Random Forests works by combining (bagging) the predictions of several classifiers, each trained on different part of the dataset.
XGBoost is similar in that it also a collection of several classifiers, but unlike Random Forest, classifiers/boosters are added sequentially, with each booster training on the errors/residuals of the previous booster, rather than the errors of the full data set.
Importantly, each tree in a Random Forest are independent, adding more trees, growing larger forests is unlikely to result in overfitting. For XGBoost, adding more boosters could eventually result in overfitting. To check for overfitting, we will split our training dataset to training and validation as outlined below.
Defining the metric
The score on the Kaggle leaderboard is evaluated by using a root mean square error (RMSE) on the logarithmic difference between the true sale price and our prediction.
Here, we define a function for evaluating the accuracy given a model/fit to the training data, and the actual data/sale price. By default we logarithmise the SalePrice to correspond with the error used to evaluate performance on Kaggle.
If no values for the targets are given, we assume that the targets can be obtained from the data object as data$SalePrice. Further, if the keyword all_errors=TRUE is given, the individual (squared) errors will be return along with total RMSE of the errors. Note this function is not at all general, and is written for convenience for this tutorial,
calc_RMSE = function(fit, data, target=NULL, log=TRUE, all_errors=FALSE){
pred = predict(fit, data, se.fit=FALSE)
if(is.null(target)) target = data$SalePrice
if(log){
pred = log(pred)
target = log(target)}
errors = (pred-target)^2
error = sqrt(mean(errors))
if(all_errors) return(list("error" = error, "errors" = errors))
else return(error)
}
Training/validation
Then, define a function for splitting the training data further to training/validation, using 80% for the training and 20% for validation.
split_data = function(df, f=0.8){
train.i = sample(nrow(df), f*nrow(df), replace = FALSE)
return(list("train" = df[train.i,], "val" = df[-train.i,]))
}
tt = get_tt(data_imp) # first split all data to training/test
s = split_data(tt$train) # the split training to training/validation
Random forests
Creating the model
Now we define and run a random forest model, using the randomForest package. We set the number of trees in each forest ntree=200, the minimum size of end nodes nodesize=10. Further we set importance=TRUE to also save the importance scores for each of the variables (see section on Feature selection below)
require(randomForest)
rf.1 = randomForest(SalePrice ~ ., data=s$train, importance=TRUE, nodesize=10, ntree=200)
Next we evaluate our model by calculating the RMSE (Log) on both train and validation.
calc_RMSE(rf.1, s$train, log=TRUE)
## [1] 0.07046209
calc_RMSE(rf.1, s$val, log=TRUE)
## [1] 0.1616448
When I run it, I get a higher error for the validation set, however, the first two significant digits of the error for both the training/validation does not change when increasing the number of trees ntree by a factor 10 (simulations not shown here), suggesting that having more trees than 200 will not result in any significant improvement, but also that adding more trees does not reduce the performance by overfitting.
rf.11 = randomForest(SalePrice ~ ., data=s$train, importance=TRUE, nodesize=10, ntree=2000)
calc_RMSE(rf.11, s$train, log=TRUE)
## [1] 0.06942862
calc_RMSE(rf.11, s$val, log=TRUE)
## [1] 0.1603187
With this, we now have a baseline result from the Random Forest model above (using ntree=200). To further analyse the Random Forest model, lets plot the (squared) errors as a function of (log) SalePrice to see if there is any region in SalePrice where the model performs best/worst.
plot(log(s$train$SalePrice), calc_RMSE(rf.1, s$train, log=TRUE, all_errors=TRUE)$errors,
xlab="SalePrice (log)", ylab="Squared log errors")
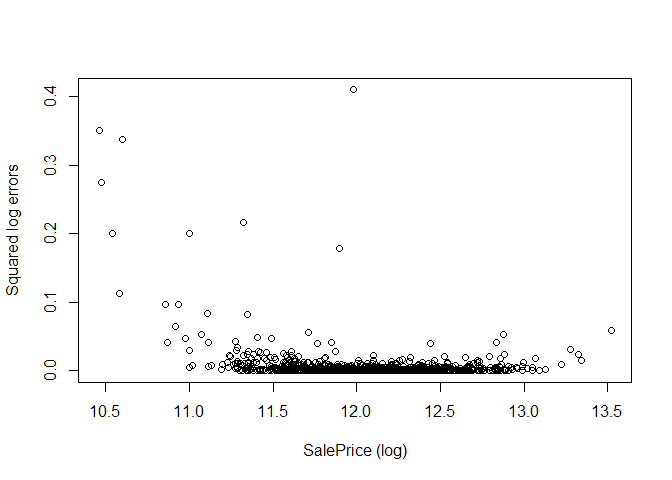
From the plot we see a (very slightly) bowl-shaped error distribution biased to the left, with higher errors for low sale prices, but also some large outlier errors throughout the range of all sale prices. One might speculate that model does not prioritize the lower values of SalePrice, since these correspond to small absolute errors with the root mean square error metric used by randomForest, while they in the log-space used by Kaggle correspond to larger relative errors.
However, my experience was that log-transforming the SalePrice did not reduce the error for the Random Forest model (code not shown here, feel free to re-run model with log(SalePrice) instead and see if any improvement is possible).
Recursive feature selection
Now, we will try to find variables which can be excluded from the analysis using recursive feature selection. This will be done in an attempt to simplify the dataset and avoid overfitting.
To this end we use the same Random Forest model as above, but extracting the importance scores for each variable to see which variables are important for the accuracy of our prediction of SalePrice on the validation set. The method randomForest in R calculates two importance scores, the first one relating to the mean decrease in the mean squared error (MSE), and the second one relating to the decrease in average node purity/Gini index. As I am not sure on how to interpret the importance score for Gini index, I will instead focus on the decrease in MSE.
A positive value for the MSE importance score %IncMSE reported by randomForest means that, when the corresponding variable is replaced with random permutation, the average MSE increases by the indicated amount. We plot the importance score (from the Random Forest model trained above) with varImpPlot(), and retrieve them with importance(),
varImpPlot(main="Variable Importance", rf.1)
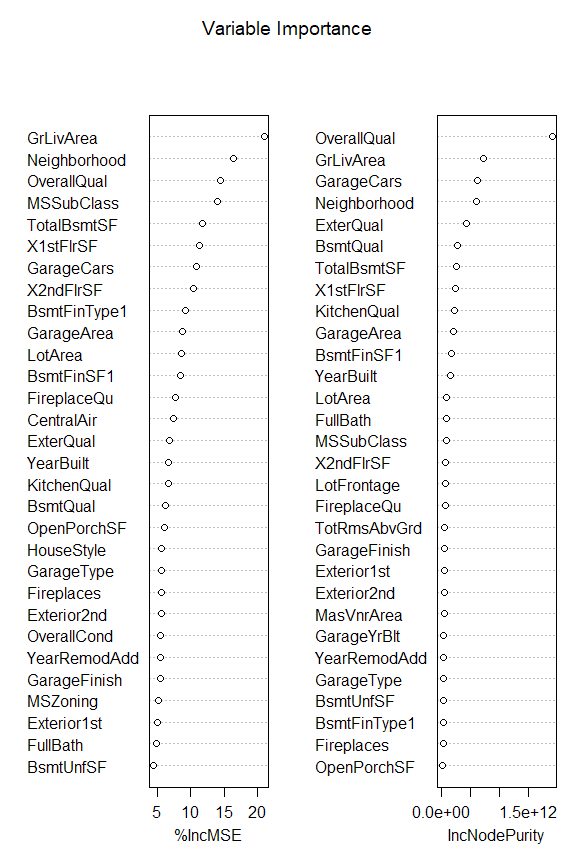
imp = importance(rf.1)
print(imp)
## %IncMSE IncNodePurity
## MSSubClass 12.84605639 8.281970e+10
## MSZoning 3.74508008 6.853436e+09
## LotFrontage 4.39107307 3.709595e+10
## LotArea 6.58381049 7.434984e+10
## Street 1.00250941 3.941767e+07
## Alley 1.91837963 1.941784e+09
## LotShape 1.64028418 7.440053e+09
## LandContour -1.58974431 7.141523e+09
## Utilities 0.00000000 8.851323e+06
## LotConfig 0.96648222 1.004356e+10
## LandSlope 0.43879877 2.259115e+09
## Neighborhood 16.76391123 8.098671e+11
## Condition1 1.17208872 4.148986e+09
## Condition2 0.28846169 1.699123e+08
## BldgType 3.34385130 3.175804e+09
## HouseStyle 4.06058325 6.876994e+09
## OverallQual 14.24597138 1.611958e+12
## OverallCond 4.00035721 2.001098e+10
## YearBuilt 5.28863450 5.641135e+10
## YearRemodAdd 5.26719822 3.938568e+10
## RoofStyle 0.51544384 5.791698e+09
## RoofMatl 1.49648998 3.706796e+09
## Exterior1st 4.51961267 3.649105e+10
## Exterior2nd 5.37819487 4.433319e+10
## MasVnrType 2.81127648 6.159362e+09
## MasVnrArea 2.32293162 3.515422e+10
## ExterQual 8.39209792 5.731137e+11
## ExterCond 1.51761350 3.469629e+09
## Foundation 5.09076149 4.319645e+09
## BsmtQual 6.54930513 1.796095e+11
## BsmtCond 3.57606675 6.405939e+09
## BsmtExposure 4.16428480 1.810295e+10
## BsmtFinType1 5.62280387 2.316542e+10
## BsmtFinSF1 9.87434266 1.490848e+11
## BsmtFinType2 1.21489582 4.703409e+09
## BsmtFinSF2 1.02294339 3.614480e+09
## BsmtUnfSF 6.30861686 2.554345e+10
## TotalBsmtSF 9.64263602 2.681220e+11
## Heating -1.12323552 3.641040e+08
## HeatingQC 1.26481158 6.323270e+09
## CentralAir 6.30340765 1.425191e+10
## Electrical 0.07832025 1.122232e+09
## X1stFlrSF 11.18438187 2.456017e+11
## X2ndFlrSF 8.20065538 1.003543e+11
## LowQualFinSF -0.09338836 2.047265e+09
## GrLivArea 21.89810237 7.764230e+11
## BsmtFullBath 4.06199330 7.935079e+09
## BsmtHalfBath -0.69358267 7.212215e+08
## FullBath 4.39229459 4.925970e+10
## HalfBath 2.16870203 8.200302e+09
## BedroomAbvGr 3.82840961 1.040001e+10
## KitchenAbvGr 1.82768672 1.993486e+09
## KitchenQual 4.95723833 1.963257e+11
## TotRmsAbvGrd 3.52734605 6.866472e+10
## Functional 2.51809690 5.000037e+09
## Fireplaces 3.84601388 2.952625e+10
## FireplaceQu 8.41291068 6.493834e+10
## GarageType 6.78367760 3.513616e+10
## GarageYrBlt 6.94059095 2.097304e+10
## GarageFinish 4.94465944 4.538122e+10
## GarageCars 6.04108289 4.898588e+11
## GarageArea 10.04695501 2.343051e+11
## GarageQual 3.20603381 6.672819e+09
## GarageCond 2.99877944 5.173845e+09
## PavedDrive 0.72832423 2.787904e+09
## WoodDeckSF 3.76277047 1.768825e+10
## OpenPorchSF 4.16496291 2.400444e+10
## EnclosedPorch 0.21423929 4.136588e+09
## X3SsnPorch 1.40214201 1.238475e+09
## ScreenPorch -0.29992571 5.181233e+09
## PoolArea 0.00000000 9.404562e+08
## PoolQC -1.00250941 1.351085e+09
## Fence 0.80252563 2.307690e+09
## MiscFeature -1.25845352 4.159301e+08
## MiscVal 1.14971518 5.949758e+08
## MoSold -1.72093675 1.094121e+10
## YrSold -0.76470137 6.650601e+09
## SaleType 2.59370364 8.831711e+09
## SaleCondition 3.25312488 6.618408e+09
It seems that there are many variables making small contributions to the total prediction, and we keep as many as possible as we there are many features and we haven’t fully explored the interdependencies.
However, some variables actually correspond to a reduction of the error if they are ignored/changed, as they have a negative value for the reported %IncMSE. We will here remove all variable with negative importance, using recursive feature elimination. I was not able to find such a function in R, so instead we will do the feature elimination ourselves.
To this end, we will create a loop where we for each iteration train a Random Forest model and find the variable with the lowest importance. If this importance is less than zero, we remove the feature from the dataset, and start a new iteration, until all variables have a positive importance.
m_data = data_imp # make a copy of the imputed data
min_imp = -1 # to run loop at least one time
while(min_imp<0){
tt = get_tt(m_data) # split all data to training/test (again)
s = split_data(tt$train) # split training to training/validation (again)
rf.temp = randomForest(SalePrice ~ ., data=s$train, importance=TRUE, nodesize=10, ntree=200)
imp = importance(rf.temp)
imp_worst = which.min(imp[,1])
min_imp = imp[imp_worst,1]
print("Variable with least importance:")
print(imp_worst)
cat("Min. importance:", min_imp, "\n" )
if(min_imp<0){
m_data = m_data %>% select(-imp_worst)
m_data$SalePrice = all_data$SalePrice # new dataset with SalePrice added back
m_data$Id = all_data$Id # new dataset with Id added back
cat("Variables in original dataset:", ncol(all_data),
". Variables in new dataset:", ncol(m_data), "\n")
}
else{
cat("No variable removed.\n")
}
}
## [1] "Variable with least importance:"
## Electrical
## 42
## Min. importance: -1.937437
## Variables in original dataset: 81 . Variables in new dataset: 80
## [1] "Variable with least importance:"
## PoolArea
## 70
## Min. importance: -1.633364
## Variables in original dataset: 81 . Variables in new dataset: 79
## [1] "Variable with least importance:"
## LotConfig
## 10
## Min. importance: -1.740129
## Variables in original dataset: 81 . Variables in new dataset: 78
## [1] "Variable with least importance:"
## LowQualFinSF
## 43
## Min. importance: -1.342515
## Variables in original dataset: 81 . Variables in new dataset: 77
## [1] "Variable with least importance:"
## RoofMatl
## 21
## Min. importance: -1.844842
## Variables in original dataset: 81 . Variables in new dataset: 76
## [1] "Variable with least importance:"
## MiscFeature
## 69
## Min. importance: -2.121014
## Variables in original dataset: 81 . Variables in new dataset: 75
## [1] "Variable with least importance:"
## YrSold
## 71
## Min. importance: -1.533271
## Variables in original dataset: 81 . Variables in new dataset: 74
## [1] "Variable with least importance:"
## RoofMatl
## 20
## Min. importance: -2.072388
## Variables in original dataset: 81 . Variables in new dataset: 73
## [1] "Variable with least importance:"
## YrSold
## 69
## Min. importance: -2.288397
## Variables in original dataset: 81 . Variables in new dataset: 72
## [1] "Variable with least importance:"
## Street
## 5
## Min. importance: -1.740176
## Variables in original dataset: 81 . Variables in new dataset: 71
## [1] "Variable with least importance:"
## LowQualFinSF
## 39
## Min. importance: -1.422772
## Variables in original dataset: 81 . Variables in new dataset: 70
## [1] "Variable with least importance:"
## MiscFeature
## 65
## Min. importance: -1.557098
## Variables in original dataset: 81 . Variables in new dataset: 69
## [1] "Variable with least importance:"
## Street
## 4
## Min. importance: -1.421266
## Variables in original dataset: 81 . Variables in new dataset: 68
## [1] "Variable with least importance:"
## RoofMatl
## 17
## Min. importance: -1.746962
## Variables in original dataset: 81 . Variables in new dataset: 67
## [1] "Variable with least importance:"
## MiscFeature
## 62
## Min. importance: -1.671692
## Variables in original dataset: 81 . Variables in new dataset: 66
## [1] "Variable with least importance:"
## LowQualFinSF
## 36
## Min. importance: -1.253548
## Variables in original dataset: 81 . Variables in new dataset: 65
## [1] "Variable with least importance:"
## LowQualFinSF
## 35
## Min. importance: -1.832373
## Variables in original dataset: 81 . Variables in new dataset: 64
## [1] "Variable with least importance:"
## MiscFeature
## 59
## Min. importance: -1.730302
## Variables in original dataset: 81 . Variables in new dataset: 63
## [1] "Variable with least importance:"
## Condition2
## 11
## Min. importance: -1.415822
## Variables in original dataset: 81 . Variables in new dataset: 62
## [1] "Variable with least importance:"
## Condition2
## 10
## Min. importance: -1.46205
## Variables in original dataset: 81 . Variables in new dataset: 61
## [1] "Variable with least importance:"
## Condition2
## 9
## Min. importance: -1.785374
## Variables in original dataset: 81 . Variables in new dataset: 60
## [1] "Variable with least importance:"
## LotConfig
## 7
## Min. importance: -1.75339
## Variables in original dataset: 81 . Variables in new dataset: 59
## [1] "Variable with least importance:"
## LowQualFinSF
## 30
## Min. importance: -2.135262
## Variables in original dataset: 81 . Variables in new dataset: 58
## [1] "Variable with least importance:"
## Condition2
## 7
## Min. importance: -1.721953
## Variables in original dataset: 81 . Variables in new dataset: 57
## [1] "Variable with least importance:"
## Street
## 3
## Min. importance: -1.002509
## Variables in original dataset: 81 . Variables in new dataset: 56
## [1] "Variable with least importance:"
## LowQualFinSF
## 27
## Min. importance: -1.038828
## Variables in original dataset: 81 . Variables in new dataset: 55
## [1] "Variable with least importance:"
## RoofMatl
## 10
## Min. importance: -2.216398
## Variables in original dataset: 81 . Variables in new dataset: 54
## [1] "Variable with least importance:"
## Street
## 2
## Min. importance: -1.681009
## Variables in original dataset: 81 . Variables in new dataset: 53
## [1] "Variable with least importance:"
## RoofMatl
## 8
## Min. importance: -1.492722
## Variables in original dataset: 81 . Variables in new dataset: 52
## [1] "Variable with least importance:"
## Condition2
## 4
## Min. importance: -2.055811
## Variables in original dataset: 81 . Variables in new dataset: 51
## [1] "Variable with least importance:"
## Condition2
## 3
## Min. importance: -2.264846
## Variables in original dataset: 81 . Variables in new dataset: 50
## [1] "Variable with least importance:"
## Condition2
## 2
## Min. importance: -2.660484
## Variables in original dataset: 81 . Variables in new dataset: 49
## [1] "Variable with least importance:"
## Condition2
## 1
## Min. importance: -1.478165
## Variables in original dataset: 81 . Variables in new dataset: 49
## [1] "Variable with least importance:"
## RoofMatl
## 4
## Min. importance: -1.189817
## Variables in original dataset: 81 . Variables in new dataset: 48
## [1] "Variable with least importance:"
## Condition2
## 1
## Min. importance: -1.802141
## Variables in original dataset: 81 . Variables in new dataset: 47
## [1] "Variable with least importance:"
## LowQualFinSF
## 18
## Min. importance: -0.1308753
## Variables in original dataset: 81 . Variables in new dataset: 46
## [1] "Variable with least importance:"
## YrSold
## 42
## Min. importance: -1.192609
## Variables in original dataset: 81 . Variables in new dataset: 45
## [1] "Variable with least importance:"
## MiscFeature
## 41
## Min. importance: -0.8270808
## Variables in original dataset: 81 . Variables in new dataset: 44
## [1] "Variable with least importance:"
## BsmtFinType2
## 15
## Min. importance: 1.160883
## No variable removed.
Now let’s calculate the RMSE (log) of our model with the new set of features to compare it to the model with the original set.
cat("Variables in original dataset:", ncol(all_data),
". Variables in new dataset:", ncol(m_data), "\n")
## Variables in original dataset: 81 . Variables in new dataset: 44
calc_RMSE(rf.temp, s$train, log=TRUE)
## [1] 0.08389441
calc_RMSE(rf.temp, s$val, log=TRUE)
## [1] 0.1741376
Interestingly, our model with removed variables performed worse on the validation compared to the original data set, despite only removing features with negative importance scores. Maybe this suggests large interdependence effects across the variables, with certain combinations of variables being important, relations cannot be seen when looking at the variables one by one.
Since we got a worse result after feature selection, we are obliged to keep the original variable set for the final model.
Submitting predictions to Kaggle
For the final Kaggle submission, we will use the full training data set (training+validation) for fitting the model and increase the number of trees to ntree=2000.
tt = get_tt(data_imp) # split all data to training/test (again)
rf.2 = randomForest(SalePrice ~ ., data=tt$train, nodesize=10, ntree=2000)
print(rf.2)
##
## Call:
## randomForest(formula = SalePrice ~ ., data = tt$train, nodesize = 10, ntree = 2000)
## Type of random forest: regression
## Number of trees: 2000
## No. of variables tried at each split: 26
##
## Mean of squared residuals: 771053379
## % Var explained: 87.77
calc_RMSE(rf.2, tt$train, log=TRUE)
## [1] 0.07160225
Looks similar to the result we got before on the training data (where we keept some observations for validation). We now use this model to get the predictions for SalePrince on the test set,
pred.test = predict(rf.2, tt$test)
Before we submit our results, we plot the distribution of the predicted (logarithmised) SalePrice in our test set (red) on top of the distribution of the (logarithmised) SalePrice in the original training data (blue), to make sure everything looks okay.
hist(log(tt$train$SalePrice), main="Training (blue), test (red) predictions", xlab = "SalePrice (log)", freq=FALSE, col=scales::alpha('blue',0.5), ylim=c(0,1.5))
hist(log(pred.test), freq=FALSE, add=T, col=scales::alpha('red',.5))

We note that the distributions look fairly similar, although there seem to be less outliers, high/low sale prices for the test predictions (red) compared to the training data (blue), but not sure if this is important.
Let’s save our test predictions and the corresponding ID’s (which we stored in the variable test_id at the beginning) as submission.csv, this file can then be submitted to Kaggle, I got the very modest score 0.150 using this model.
subm = cbind(test_id, pred.test)
colnames(subm) = c("Id", "SalePrice")
write.csv(subm, "submission.csv", row.names=FALSE)
EDIT: When submitting the result to kaggle, I use the kaggle CLI. Whenever you make a submission you also have to provide the name of the competition you want to provide a solution for, the file you want to send, and a message, which I like to set to something as descriptive as possible to keep track of what I’ve tried. Follow the information obtained by running kaggle --help for more information. For me, I would likely submit the above result with
# kaggle competitions submit -c "house-prices-advanced-regression-techniques" -f "submission.csv" -m "randomForest ntree=2000 nodesize=10"
XGBoost
We will also train a model based on XGBoost. We begin by importing the xgboost package (install if need be, it is available at CRAN) which provide an R interface to the XGBoost algorithm.
require(xgboost)
## Loading required package: xgboost
##
## Attaching package: 'xgboost'
## The following object is masked from 'package:dplyr':
##
## slice
XGBoost, short for extreme gradient boosting, uses boosting which sequentially adds models that trains on/corrects the errors made by previous models. As we will see it can be a powerful method able to bring about great results at relatively low computational cost, although with a risk of overfitting.
Data preparation
We start by retrieving new training/validation/test data sets. Here, we need to consider that xgboost, unlike randomForest, only accepts numerical variables, as such we need to somehow recode our categorical values into integers. This can be done e.g., using one-hot encoding, where the presence of each category is indicated by a 1 and its absence is indicated by a 0.
Fortunately for us, this is very easy to do with the package fastDummies.
tt = get_tt(data_imp) # get training/test from imputed data
# one-hot encoding of categorical variables
require("fastDummies")
## Loading required package: fastDummies
tt$train = dummy_cols(tt$train, remove_selected_columns =TRUE, remove_first_dummy=TRUE)
tt$test = dummy_cols(tt$test, remove_selected_columns =TRUE, remove_first_dummy=TRUE)
When creating the dummy columns we set remove_selected_columns=TRUE to make sure we also discard the old columns with factors. I also set the remove_first_dummy=TRUE, meaning that the first category is removed for each variable, as this somewhat reduces the amount of columns in our final matrix. Let’s continue and get the train/validation/test sets.
s = split_data(tt$train) # split data to train/test
train = s$train
val = s$val
test = tt$test
The package xgboost wants data in the DMatrix format. A DMatrix can be created from a matrix X of features (independent variables) and vector y of the corresponding targets (dependent variable).
To this end we will extract X (features) and y (target) for the training/validation/test sets and create the DMatrices we need for xgboost.
For xgboost, I found better results logarithmising the SalePrice before training the model, so this is what we’ll be doing here.
train_y = log(train$SalePrice)
train_X = data.matrix(subset(train, select = - SalePrice))
val_y = log(val$SalePrice)
val_X = data.matrix(subset(val, select = - SalePrice))
test_y = log(test$SalePrice)
test_X = data.matrix(subset(test, select = - SalePrice))
dtrain = xgb.DMatrix(data = train_X, label = train_y)
dtest = xgb.DMatrix(data = test_X, label = test_y)
Defining the model
Now we set the parameters for running xgboost. The ones we will set here is max_depth, maximum depth of each tree (default=6), lambda and alpha which are the regularization strengths for L1 and L2 regularization (default=0 for both), min_child_weight which for linear regression corresponds to the minimum number of instances in each node (default=1), eta meaning the learning rate (default=0.3). For the objective function, I found the squarederror to work well (objective=reg:squarederror).
We begin by setting the parameters at the default values and fit the model, to get a baseline result.
xgb.paras=list(max_depth=6,lambda=0.0,alpha=0.0,min_child_weight=0, booster ="gbtree",
eta=0.3, objective="reg:squarederror")
xgb.fit0 = xgboost(data = dtrain, nrounds=300,params=xgb.paras, nthread = 6, verbose=0)
Then calculate the error on both training and validation
calc_RMSE(xgb.fit0, train_X, target=train_y, log=FALSE)
## [1] 0.001065989
calc_RMSE(xgb.fit0, val_X, target=val_y, log=FALSE)
## [1] 0.133795
Note that although we were able to get a very low error on the training data, the error on the validation was much higher. After some behind-the-scenes experimenting/scanning of parameter values, I found the parameters below to work better, providing a lower error on the validation set, feel free to see if you can find any improvements.
xgb.paras=list(max_depth=3,lambda=0.01,alpha=0.01,min_child_weight=0, booster ="gbtree",
eta=0.01, objective="reg:squarederror")
xgb.fit = xgboost(data = dtrain, nrounds=2000,params=xgb.paras, nthread = 6, verbose=0)
Again, when calculating the errors for training and validation, the above parameters yields a somewhat lower validation error. As the training error also is higher, it might be that we avoided some overfitting, indicating a better model with less variance.
calc_RMSE(xgb.fit, train_X, target=train_y, log=FALSE)
## [1] 0.06326491
calc_RMSE(xgb.fit, val_X, target=val_y, log=FALSE)
## [1] 0.1187995
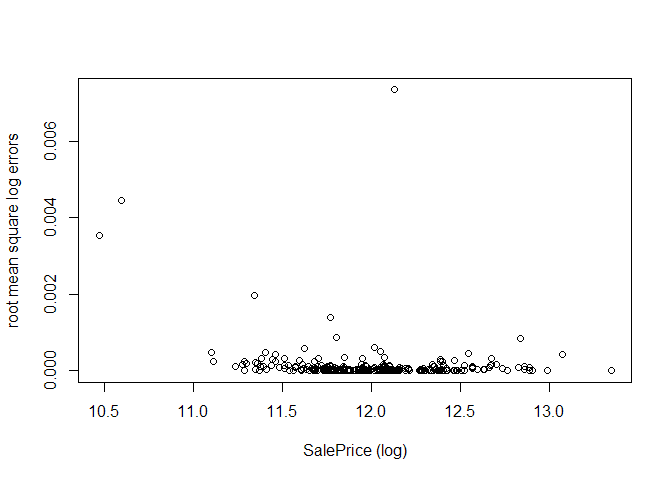
Now, we analyse the model by plotting the log-errors as a function of the log-SalePrice, as was done for the Random Forests. In the validation set, the errors seem evenly distributed, with no clear bias towards being better at predicting high/low sale prices, but with some outliers where the prediction was off by larger amounts.
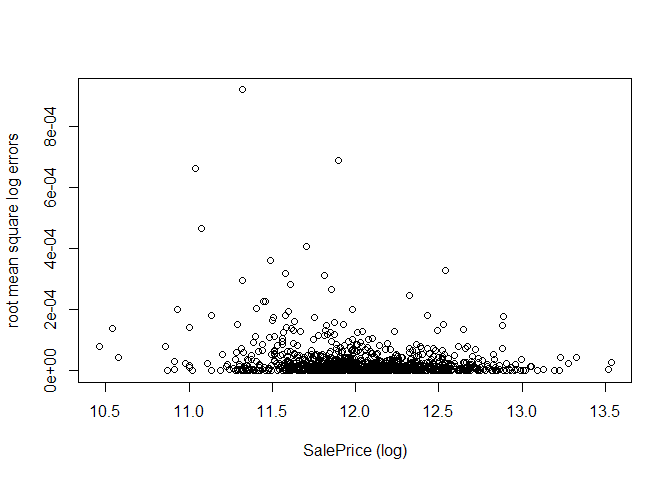
plot(train_y, calc_RMSE(xgb.fit, train_X, target=train_y, log=TRUE, all_errors=TRUE)$errors,
xlab="SalePrice (log)", ylab="root mean square log errors")
plot(val_y, calc_RMSE(xgb.fit, val_X, target=val_y, log=TRUE, all_errors=TRUE)$errors,
xlab="SalePrice (log)", ylab="root mean square log errors")
Create final model and submit result
For the final model used in the Kaggle submission, we train on all available training data (training + validation) with the same parameters as the best model found above.
trainall_y = log(tt$train$SalePrice)
trainall_X = data.matrix(subset(tt$train, select = - SalePrice))
dtrainall = xgb.DMatrix(data = trainall_X, label = trainall_y)
xgb.fitall = xgboost(data = dtrainall, nrounds=2000,params=xgb.paras, nthread = 6, verbose=0)
To get predictions on test set, we exponentiate to get back the price in dollars.
pred2.test = exp(predict(xgb.fitall, dtest))
To check the sanity of our result on the test set, we plot the distribution of value of salePrice in the training data (blue) and the distribution of predicted SalePrice for the test set using xgboost (green)
hist(log(tt$train$SalePrice), main="Training (blue), test (green) predictions",
xlab = "SalePrice (log)", freq=FALSE, col=scales::alpha('blue',0.5), ylim=c(0,1.5))
hist(log(pred2.test), freq=FALSE, add=T, col=scales::alpha('green',.5))
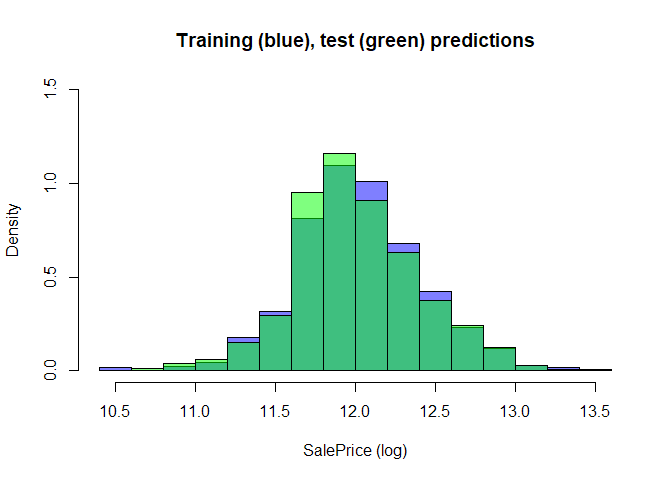
This is just to quickly check the results before submitting, in order to see that we haven’t accidentally exponentiated the target an extra time or something else. As they seem similar enough, we then save the result and submit to Kaggle.
subm = cbind(test_id, pred2.test)
colnames(subm) = c("Id", "SalePrice")
write.csv(subm, "submission.csv", row.names=FALSE)
The best score I was able to get using this approach and these parameter values was 0.131 when submitting to the Kaggle leaderboard. Interestingly, a substantial improvement to the result from the Random Forest model, showing how in this case XGBoost is able to improve the prediction even further compared to RandomForests, when building models sequentially training on the errors of the previous models.
Conclusion
At the end of this tutorial, we have made a submission to Kaggle that deals with a varied set of features related to housing prices, in which we had to deal with missing values and where we predicted the sale price using Random Forests and XGBoost.
To handle the missing values, we used the package missForest available in R which imputed the missing values with a Random Forest algorithm. Though not touched upon in this tutorial, my own casual observation is that missForest does improve accuracy of our final score compared to that of a simpler imputation (e.g. replacing all missing values with their means/mode), but at the cost of time-consuming computations, and my feeling is that in a production environment where new data is continuously added, one should use the simpler, less computationally-intensive way of imputation using the means/modes.
Moving on, we found that the best score on the test set was obtained with a XGBoost model. We attempted to reduce the number of features in our data set with recursive feature selection (RFE), where we only kept features that improved the out-of-bag (OOB) error of a recursively trained Random Forest model. However, as the end result of the RFE was a model with less accuracy on the validation set, we kept all variables for the final model. Though the RFE approach was unsuccessful and reduced the accuracy of the final model, the results presented here could provide some insight into the dataset, e.g. suggesting important variables.
Appendix: Catboost
With catboost, which is a gradient boosting method specializing on categorical/mixed data, developed by https://en.wikipedia.org/wiki/Yandex, even better results were possible, out-of-the-box.
As I was impressed with the performance, I will give a quick introduction on how to install and run a catboost model here.
Installation
The documentation https://catboost.ai/docs/installation/r-installation-binary-installation.html tells us to install catboost with
# install.packages('devtools')
# devtools::install_url('BINARY_URL', INSTALL_opts = c("--no-multiarch"))
where BINARY_URL is a link to the version you want to install. For example, the latest version at the time of writing (Windows) is https://github.com/catboost/catboost/releases/download/v0.24.4/catboost-R-Windows-0.24.4.tgz see e.g. https://github.com/catboost/catboost/releases.
Unfortunately version 0.24.4 did not seem to work for me, as I seem to get a similar error as in https://github.com/catboost/catboost/issues/1525, Therefore, as a bonus, here are the R-commands required to unload the catboost package from the current R-environment and remove the package, so you can reinstall a new version, after restarting the R session,
# detach("package:catboost", unload=TRUE) # detach catboost from current R session
# remove.packages("catboost") # uninstall catboost
As version 0.24.3 seems to work fine, we instead install this version, and load it
# devtools::install_url('https://github.com/catboost/catboost/releases/download/v0.24.3/catboost-R-Windows-0.24.3.tgz')
require("catboost")
## Loading required package: catboost
Preparing the data
As before we split the data to training/test, and then we split training to training/validation.
tt = get_tt(data_imp) # get training/test data
s = split_data(tt$train) # split training to training/validation
Now we define the different datasets, training data, validation data, all training data (validation+training) and test data, in the format catboost wants,
train_pool = catboost.load_pool(data = select(s$train, -c("SalePrice")), label = log(s$train$SalePrice))
val_pool = catboost.load_pool(data = select(s$val, -c("SalePrice")), label = log(s$val$SalePrice))
alltrain_pool = catboost.load_pool(data = select(tt$train, -c("SalePrice")), label = log(tt$train$SalePrice))
test_pool = catboost.load_pool(data = select(tt$test, -c("SalePrice")), label = log(tt$test$SalePrice))
Training the model
After some more hyperparameter tuning, I found a good parameter set to be depth = 4, learning_rate = 0.01, iterations = 5000, l2_leaf_reg = 1, rsm = 0.1, border_count = 254 and early_stopping_rounds=200. I will not go into the meanings of this parameters, but please see the catboost documentation for more details, and possibly find your own, even better, values. Now we will train the model. Note that the catboost.train function takes both a training dataset and a validation dataset, allowing us to monitor the performance on the validation set during the training.
cb.paras = list(loss_function = 'RMSE', iterations = 5000,
metric_period=100, depth=4, rsm=0.1,
border_count=254, learning_rate=0.01,
l2_leaf_reg=1, early_stopping_rounds=200)
cb.model = catboost.train(train_pool, val_pool, params = cb.paras)
## Warning: Overfitting detector is active, thus evaluation metric is calculated on every iteration. 'metric_period' is ignored for evaluation metric.
## 0: learn: 0.3955673 test: 0.4034571 best: 0.4034571 (0) total: 53.2ms remaining: 4m 26s
## 100: learn: 0.2467607 test: 0.2512793 best: 0.2512793 (100) total: 940ms remaining: 45.6s
## 200: learn: 0.1836174 test: 0.1873397 best: 0.1873397 (200) total: 1.84s remaining: 43.9s
## 300: learn: 0.1555228 test: 0.1617281 best: 0.1617281 (300) total: 2.75s remaining: 42.9s
## 400: learn: 0.1409895 test: 0.1493931 best: 0.1493931 (400) total: 3.65s remaining: 41.9s
## 500: learn: 0.1315766 test: 0.1419048 best: 0.1419048 (500) total: 4.55s remaining: 40.9s
## 600: learn: 0.1246155 test: 0.1372702 best: 0.1372702 (600) total: 5.45s remaining: 39.9s
## 700: learn: 0.1187299 test: 0.1332261 best: 0.1332261 (700) total: 6.33s remaining: 38.9s
## 800: learn: 0.1135539 test: 0.1299086 best: 0.1299086 (800) total: 7.23s remaining: 37.9s
## 900: learn: 0.1092132 test: 0.1273869 best: 0.1273869 (900) total: 8.12s remaining: 37s
## 1000: learn: 0.1052751 test: 0.1254555 best: 0.1254555 (998) total: 9.03s remaining: 36.1s
## 1100: learn: 0.1021420 test: 0.1238649 best: 0.1238565 (1099) total: 9.94s remaining: 35.2s
## 1200: learn: 0.0996795 test: 0.1227769 best: 0.1227736 (1199) total: 10.9s remaining: 34.4s
## 1300: learn: 0.0973729 test: 0.1218977 best: 0.1218921 (1298) total: 11.8s remaining: 33.4s
## 1400: learn: 0.0953014 test: 0.1210086 best: 0.1210085 (1399) total: 12.7s remaining: 32.5s
## 1500: learn: 0.0932589 test: 0.1203908 best: 0.1203908 (1500) total: 13.6s remaining: 31.6s
## 1600: learn: 0.0916012 test: 0.1197485 best: 0.1197455 (1596) total: 14.5s remaining: 30.7s
## 1700: learn: 0.0900183 test: 0.1193086 best: 0.1193086 (1700) total: 15.4s remaining: 29.8s
## 1800: learn: 0.0884368 test: 0.1187568 best: 0.1187568 (1800) total: 16.3s remaining: 28.9s
## 1900: learn: 0.0869875 test: 0.1183434 best: 0.1183434 (1900) total: 17.2s remaining: 28s
## 2000: learn: 0.0857432 test: 0.1180121 best: 0.1180121 (2000) total: 18.1s remaining: 27.1s
## 2100: learn: 0.0845322 test: 0.1177919 best: 0.1177919 (2100) total: 19s remaining: 26.2s
## 2200: learn: 0.0834684 test: 0.1175702 best: 0.1175670 (2197) total: 19.9s remaining: 25.3s
## 2300: learn: 0.0824500 test: 0.1174580 best: 0.1174477 (2298) total: 20.8s remaining: 24.4s
## 2400: learn: 0.0814324 test: 0.1173079 best: 0.1173079 (2400) total: 21.7s remaining: 23.5s
## 2500: learn: 0.0804397 test: 0.1171058 best: 0.1171034 (2491) total: 22.6s remaining: 22.6s
## 2600: learn: 0.0794627 test: 0.1169852 best: 0.1169852 (2600) total: 23.5s remaining: 21.7s
## 2700: learn: 0.0784878 test: 0.1169022 best: 0.1168870 (2650) total: 24.4s remaining: 20.8s
## 2800: learn: 0.0776579 test: 0.1167957 best: 0.1167957 (2800) total: 25.3s remaining: 19.9s
## 2900: learn: 0.0767674 test: 0.1167102 best: 0.1167095 (2899) total: 26.2s remaining: 19s
## 3000: learn: 0.0758981 test: 0.1166598 best: 0.1166439 (2986) total: 27.1s remaining: 18.1s
## 3100: learn: 0.0750977 test: 0.1166367 best: 0.1166183 (3075) total: 28s remaining: 17.2s
## 3200: learn: 0.0743912 test: 0.1165727 best: 0.1165596 (3190) total: 28.9s remaining: 16.3s
## 3300: learn: 0.0736714 test: 0.1165328 best: 0.1165268 (3245) total: 29.8s remaining: 15.4s
## 3400: learn: 0.0729281 test: 0.1164713 best: 0.1164681 (3399) total: 30.7s remaining: 14.4s
## 3500: learn: 0.0722066 test: 0.1164088 best: 0.1163956 (3473) total: 31.6s remaining: 13.5s
## 3600: learn: 0.0714780 test: 0.1164251 best: 0.1163956 (3473) total: 32.5s remaining: 12.6s
## 3700: learn: 0.0706155 test: 0.1163951 best: 0.1163863 (3617) total: 33.4s remaining: 11.7s
## 3800: learn: 0.0698717 test: 0.1162976 best: 0.1162955 (3798) total: 34.3s remaining: 10.8s
## 3900: learn: 0.0691744 test: 0.1162971 best: 0.1162836 (3888) total: 35.2s remaining: 9.93s
## 4000: learn: 0.0685293 test: 0.1162951 best: 0.1162812 (3933) total: 36.2s remaining: 9.03s
## 4100: learn: 0.0678657 test: 0.1163229 best: 0.1162812 (3933) total: 37.1s remaining: 8.13s
## Stopped by overfitting detector (200 iterations wait)
##
## bestTest = 0.1162811684
## bestIteration = 3933
##
## Shrink model to first 3934 iterations.
To verify our result, we make a prediction and calculate the RMSE log error on the validation set
prediction = catboost.predict(cb.model, val_pool)
logrmse_val = (mean( ((prediction-log(s$val$SalePrice))**2)))**0.5
cat("Log error (validation):", logrmse_val)
## Log error (validation): 0.1162812
Seems good! Now we train the model on all training data (training + validation). We set the second parameter in catboost.train to NULL as we don’t supply any validation data.
cb.modelf = catboost.train(alltrain_pool, NULL, params = cb.paras)
## 0: learn: 0.3972835 total: 4.03ms remaining: 20.1s
## 100: learn: 0.2469311 total: 916ms remaining: 44.4s
## 200: learn: 0.1844478 total: 1.83s remaining: 43.7s
## 300: learn: 0.1559904 total: 2.75s remaining: 42.9s
## 400: learn: 0.1407558 total: 3.64s remaining: 41.8s
## 500: learn: 0.1309642 total: 4.54s remaining: 40.8s
## 600: learn: 0.1239503 total: 5.45s remaining: 39.9s
## 700: learn: 0.1187411 total: 6.36s remaining: 39s
## 800: learn: 0.1141205 total: 7.25s remaining: 38s
## 900: learn: 0.1103811 total: 8.16s remaining: 37.1s
## 1000: learn: 0.1071739 total: 9.07s remaining: 36.2s
## 1100: learn: 0.1043081 total: 9.97s remaining: 35.3s
## 1200: learn: 0.1021137 total: 10.9s remaining: 34.4s
## 1300: learn: 0.0999649 total: 11.8s remaining: 33.5s
## 1400: learn: 0.0980403 total: 12.7s remaining: 32.6s
## 1500: learn: 0.0963822 total: 13.6s remaining: 31.7s
## 1600: learn: 0.0948042 total: 14.5s remaining: 30.8s
## 1700: learn: 0.0931807 total: 15.4s remaining: 29.9s
## 1800: learn: 0.0916737 total: 16.3s remaining: 29s
## 1900: learn: 0.0904573 total: 17.3s remaining: 28.1s
## 2000: learn: 0.0891984 total: 18.1s remaining: 27.2s
## 2100: learn: 0.0879630 total: 19.1s remaining: 26.3s
## 2200: learn: 0.0868724 total: 19.9s remaining: 25.4s
## 2300: learn: 0.0858766 total: 20.8s remaining: 24.5s
## 2400: learn: 0.0849283 total: 21.8s remaining: 23.5s
## 2500: learn: 0.0839723 total: 22.7s remaining: 22.6s
## 2600: learn: 0.0830420 total: 23.6s remaining: 21.7s
## 2700: learn: 0.0821909 total: 24.5s remaining: 20.8s
## 2800: learn: 0.0813601 total: 25.4s remaining: 19.9s
## 2900: learn: 0.0805193 total: 26.3s remaining: 19s
## 3000: learn: 0.0796804 total: 27.2s remaining: 18.1s
## 3100: learn: 0.0789579 total: 28.1s remaining: 17.2s
## 3200: learn: 0.0782867 total: 29s remaining: 16.3s
## 3300: learn: 0.0776087 total: 29.9s remaining: 15.4s
## 3400: learn: 0.0768693 total: 30.8s remaining: 14.5s
## 3500: learn: 0.0762374 total: 31.7s remaining: 13.6s
## 3600: learn: 0.0755818 total: 32.6s remaining: 12.7s
## 3700: learn: 0.0749239 total: 33.5s remaining: 11.8s
## 3800: learn: 0.0742657 total: 34.5s remaining: 10.9s
## 3900: learn: 0.0736331 total: 35.4s remaining: 9.96s
## 4000: learn: 0.0730605 total: 36.3s remaining: 9.06s
## 4100: learn: 0.0724690 total: 37.2s remaining: 8.16s
## 4200: learn: 0.0717551 total: 38.1s remaining: 7.25s
## 4300: learn: 0.0711890 total: 39s remaining: 6.34s
## 4400: learn: 0.0706128 total: 39.9s remaining: 5.44s
## 4500: learn: 0.0700200 total: 40.9s remaining: 4.53s
## 4600: learn: 0.0694611 total: 41.8s remaining: 3.62s
## 4700: learn: 0.0689162 total: 42.7s remaining: 2.71s
## 4800: learn: 0.0683931 total: 43.6s remaining: 1.81s
## 4900: learn: 0.0678758 total: 44.5s remaining: 899ms
## 4999: learn: 0.0673540 total: 45.4s remaining: 0us
Obtaining predictions on test set
Predict the SalePrice on the test data with the above model,
pred3.test = exp(catboost.predict(cb.model, test_pool))
As before plot the true SalePrice for the training data (blue), versus the test prediction (green) for SalePrice to make sure we have not made any errors,
hist(log(tt$train$SalePrice), main="Training (blue), test (green) predictions",
xlab = "SalePrice (log)", freq=FALSE, col=scales::alpha('blue',0.5), ylim=c(0,1.5))
hist(log(pred3.test), freq=FALSE, add=T, col=scales::alpha('green',.5))

Save file and submit to Kaggle
As it looks fine we save it to a file that we submit to Kaggle.
subm = cbind(test_id, pred3.test)
colnames(subm) = c("Id", "SalePrice")
write.csv(subm, "submission.csv", row.names=FALSE)
# kaggle competitions submit -c "house-prices-advanced-regression-techniques" -f "submission.csv" -m "catboost! paraset al1"
With the catboost model above, I got an error of 0.122 on the Kaggle test set, which is pretty huge improvement from the xgboost result of 0.131, considering both models were implemented as-is except for a similar hyperparameter tuning process for both, based on cross-validation/parameter scanning (caret package).